ENERGIA LIBERA IN CHIMICA
Settembre 18, 2024In una reazione chimica l’energia del suo contenuto termico non è tutta disponibile per effettuare lavoro, ciò perché il sistema stesso ne utilizza una sua parte.L’energia libera è definita da
G=H-TS che possiamo anche scrivere G= E+PV -TS
dove
- E = energia interna ( joule)
- P= pressione ( pascal)
- V= volume (litri)
- T= temperatura ( kelvin)
- S=is entropia ( joule/kelvin)
- H= entalpia
- S= entropia (joule)
Essendo H ed S funzioni di stato la loro somma o differenza è sempre una funzione di Stato quindi G è una funzione di stato che dipende esclusivamente dallo stao iniziale e finale del sistema in esame.
L’energia libera è molto utile per quanto riguarda i fenomeni chimici : infatti Gibbs la definì ” Available Energy” e riassume in sé il primo ed il secondo principio della termodinamica ed è alla base dello studio degli equilibri chimici.
Una reazione chimica viene favorita o sfavorita a seconda dell’entalpia e dell’entropia di reazione.Infatti in una reazione esotermica che comporta un aumento dell’ordine, essendo i prodotti a contenuto entalpico più basso, la variazione di entalpia tende a rendere la reazione spontanea, mentre la variazione di entropia tende ad ostacolare la reazione stessa essendo la variazione di entropia di una reazione spontanea maggiore di zero.Si deduce quindi che per una reazione chimica possiamo scrivere
ΔG = ΔH – TΔS
Se consideriamo una reazione spontanea sappiamo che TΔS è maggiore di ΔH per cui ne risulta un valore di ΔG negativo, mentra per una reazione non spontanea ΔG è positivo, nel caso in cui la reazione sia in equilibrio ΔG=0.
In una trasformazione spontanea ∆G è sempre negativa quindi se ∆G < 0 la reazione è definita esoergonica cioè avviene con produzione di calore (il ΔH dei prodotti è minore del ΔH dei reagenti) ; una reazione con ∆G > 0 è invece definita endoergonica cioè avviene con assorbimento di calore dall’esterno (il ΔH dei prodotti è maggiore del ΔH dei reagenti) . Anche la temperatura assume un ruolo importante nelle trasformazioni chimiche, infatti, se una reazione avviene a bassa temperatura e comporta una piccola variazione di entropia, il termine T∆S sarà trascurabile e ∆G dipenderà in gran parte da ∆H per cui si deduce che le reazioni chimiche che avvengono spontaneamente a temperatura ambiente hanno un ∆H negativo.Da ciò si evince anche che Reazioni fortemente endotermiche possono avvenire soltanto se il termine T∆S è elevato e questo si verifica quando la temperatura è elevata o se vi è un considerevole aumento di entropia e si può dire che :
“L’aumento di temperatura favorisce le reazioni endotermiche e sfavorisce quelle esotermiche”.
Se ∆H e ∆S hanno lo stesso segno, vi sarà una temperatura alla quale ∆H e T∆S saranno numericamente uguali e ∆G sarà esattamente uguale a zero: tale stato è la definizione termodinamica di un equilibrio chimico. All’equilibrio, il valore dell’energia libera di Gibbs corrisponde a un minimo di G per il sistema in esame cioè ΔG = 0 . Riassumendo si ha:
| ∆H | ∆S | ∆G | Previsione sulla reazione |
| – | + | – | sempre spontanea |
| + | + | + o – | spontanea ad alte temperature |
| – | – | + o – | spontanea a basse temperature |
| + | – | + | mai spontanea |
| ∆H = T∆S | 0 | all’equilibrio | |
esempio
Calcolare ∆G a 290 K per la reazione: 2NO_{(g)} + O2(g) → 2NO2(g) sapendo che
- ∆H = -120 kJ
- ∆S = -150 JK -1
soluzione
Δ S = -150 J/K x (1 KJ /1000) = -0,15 kJ/K
∆G= -120 kJ – (290 K )(-0.150 kJ/K) = 120 kJ + 43 kJ
∆G= – 776 kJ
ENERGIA LIBERA E COSTANTE DI EQUILIBRIO
L’energia libera di una reazione è pari alla differenza tra l’energia libera molare dei prodotti e quella dei reagenti alla pressione parziale o alla concentrazione che essi assumono moltiplicata per il coefficiente stechiometrico di ogni partecipante alla reazione. Per una generica reazione
aA + bB <=> cC + dD
ΔGreaz= ∑ ΔGprodotti – ∑ΔGreagenti
Consideriamo una reazione in fase gassosa
sappiamo che
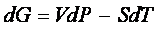
e per un processo infinitesimo a temperatura costante,
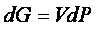
ma per un gas ideale
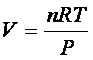
per cui
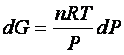
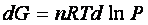
La variazione di energia libera in una trasformazione finita tra gli estremi G0e P0, che rappresentano l’energia libera e la pressione in uno stato standard opportunamente scelto e i corrispondenti valori in qualunque altro stato G e P è ottenuta integrando quest’ultima espressione:
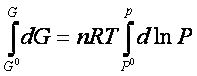 cioè
cioè
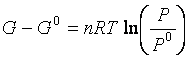
e poiché per la pressione si è scelto come stato standard il valore P0 = 1atm,
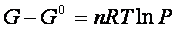
Questa equazione indica la ΔG che un gas subisce nel passaggio dalla pressione di 1 atm (da uno stato standard) , al valore generico P finale.
Se consideriamo una miscela di gas, ognuno con pressione parziale pi, si ha :
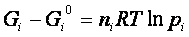
.Per una reazione in fase gassosa:
νa A + νb B <==> νc C + νd D
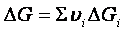
ΔGi sono le variazioni delle energie libere dei gas
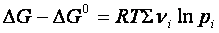
Se la reazione giunge all’equilibrio, ΔG =0, perciò
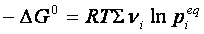
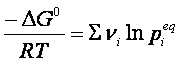
Nella quale si vede che a temperatura costante, il primo membro deve essere costante, essendo ΔG0 indipendente dalla temperatura. Perciò lo sarà anche il secondo membro dell’ espressione, che, per la proprietà dei logaritmi, può essere scritto nel seguente modo:
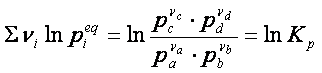
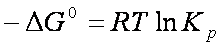
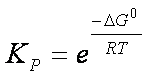
pertanto
ΔG° = – RT ln Keq
Questa espressione permette il calcolo della Keq di una reazione se si conosce la variazione di energia libera ad una data temperatura.
ESERCIZI
1- calcolare l’energia libera A 25° della reazione
N2(g) + 3 H2(g) <=> 2NH3(g)
se PN2 = 100 atm ; PH2= 40 atm ; PNH3= 60 atm
ΔG°NH3 = – 16,4 KJ
soluzione
sappiamo che ΔG=ΔG° + RTln(Q) e che ΔG° = ΔG° prodotti – ΔG° reagenti
pertanto ΔG° = 2 x ΔG°NH3 – 3 x ΔG°H2 + ΔG°N2
però sappiamo che quando le sostanze si trovano allo stato elementare il ΔG° =0 quindi
ΔG° = 2 x ΔG°NH3 – 3 x 0 + 0 =2 x ΔG°NH3
dai dati si ha 2 x ΔG°NH3 = -32,8 KJ
inoltre dalla reazione data si ha Q= (PNH3)2 / PN2 x ( PH2)3
Q= (60)2 / 100 x (40)3
Q= 5,63 x 10-4
R= 8.314 J/mol quindi
ΔG = -32,8 KJ /mol + 8.314 J/mol x 298 K x ln (5,63 x 10-4 ) x 1 KJ/1000J
ΔG = – 51,3 KJ/mol
Dobbiamo notare che questo calcolo viene effettuato quando la reazione NON è all’equilibrio, infatti all’equilibrio sappiamo che
ΔG = 0 quindi
0 =ΔG° + RTln Keq
ΔG° = – RTln Keq
La Keq per la reazione data sopra è Keq=5,6 x 10-5 che è diversa da Q= 5,63 x 10-4
