IBRIDIZZAZIONE DEGLI ORBITALI ATOMICI – calcolo completo per ibridi SP3

Gennaio 21, 2024 By wp_7813724

GLI ORBITALI ATOMICI

Un orbitale atomico (detto anche funzione orbitale) è una funzione matematica generalmente indicata con la lettera greca Ψ che descrive un elettrone che si muove intorno al nucleo. Ogni orbitale atomico è rappresentato da un’espressione matematica che sostituita nella Equazione di Schrödinger

H Ψ = E Ψ

dà come risultato un valore di E diverso da zero.

La forma matematica di un orbitale atomico è costituita da due parti di cui una cosiddetta radiale cioè che dipende dalla distanza r dal nucleo ed un’altra cosiddetta angolare (esprimendo le coordinate in coordinate polari )

In cui si ha :

x = r sen(θ) cos(φ)
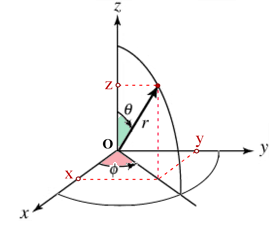
y = r sen(θ) sen(φ)
z = r cos(θ)

dai calcoli effettuati sostituendo le funzioni nell’equazione di Schrödinger osserviamo che la forma matematica dell’orbitale più vicino al nucleo (che si indica con 1 S) è :

Ψ1S = 1 / √π ( Z/a)^3/2x e^-Zr/a

e se consideriamo l’atomo di idrogeno con un solo elettrone si ha :

Ψ1S = 1 / √π ( 1/a)^3/2x e^-r/a

dove a= raggio di Bohr che in unità atomiche è a= 0,5293 A° (angstrom).

Queste funzioni di tipo S poiché dipendono solo dalla variabile r possiedono una simmetria sferica e la densità elettronica è anche sferica (la densità elettronica non è altro che quello che viene chiamato in modo non appropriato Orbitale atomico!)

l’orbitale 2 S per l’idrogeno ha una forma matematica simile

Ψ2S = 1 /4 √2π ( 1/a)^3/2x (r/a -2)e^-r/2a

gli orbitali di tipo P invece possiedono oltre che la parte radiale anche la parte angolare ed hanno la forma matematica seguente:

Ψ2P (z) = 1 / 4√2π ( 1/a)^3/2x r/a x e^{_{^-r/2a cos θ}}

Ψ2P (x) = 1 / 4√2π ( 1/a)^3/2x r/a x e^-r/2a sen θ cos φ

^{Ψ2P (y) = 1 / 4√2π ( 1/a)^3/2x r/a x e-r/2a sen θ sen φ}

Per gli orbitali di tipo s la parte angolare rimane costante, cioà è indipendente dall’angolo Θ e Φ. Per l’orbitale 2pz la parte angolare dipende solo l’angolo Θ; questo significa che l’orbitale ha simmetria cilindrica attorno all’asse z, pertanto la rotazione in Φ produce sempre lo stesso valore ( la parte angolare caratterizza la forma degli orbitali).

In generale la funzione orbitale è caratterizzata da numeri che in generale si indicano con

n, l ,m, S

$\psi _{n,\ell ,m}^{\text{real}}(r,\theta ,\phi )=R_{nl}(r)Y_{\ell m}(\theta ,\phi )$

che vengono chiamati numeri quantici.

perchà la funzione Ψ sia soluzione dell’equazione di Schrödinger i numeri quantici devono assumere valori ben precisi in relazione tra loro infatti:

n rappresenta il numero quantico PRINCIPALE (cioè il livello di energia in cui si trova l’elettrone)

essendo possibili infiniti livelli n può assumere valori da 1 ad infinito

l rappresenta il numero quantico angolare (cioè il momento angolare dell’elettrone nell’atomo e può assumere tutti i valori interi da 0 a n-1)

m è detto numero quantico magnetico, definisce la componente del
momento angolare, quando si applica un campo magnetico, nella direzione del campo magnetico applicato,
m può assumere tutti i valori interi da –l a +l compreso lo 0
ms è il numero quantico di spin, rappresenta la proprietà magnetica intrinseca dell’elettrone.

ms può assumere solo i due valori associati con la rotazione intorno al proprio asse:

+ ½ e – ½ (di h/2π) associati ai due versi di rotazione orario e antiorario.

	$m = -3$	$m = -2$	$m = -1$	$m = 0$	$m = +1$	$m = +2$	$m = +3$
$\ell =0$				${\text{s}}$
$\ell =1$			${\text{p}}_{y}$	${\text{p}}_{z}$	${\text{p}}_{x}$
$\ell =2$		${\text{d}}_{xy}$	${\text{d}}_{yz}$	${\text{d}}_{z^{2}}$	${\text{d}}_{xz}$	${\text{d}}_{x^{2}-y^{2}}$
$\ell =3$	${\text{f}}_{y(3x^{2}-y^{2})}$	${\text{f}}_{xyz}$	${\text{f}}_{yz^{2}}$	${\text{f}}_{z^{3}}$	${\text{f}}_{xz^{2}}$	${\text{f}}_{z(x^{2}-y^{2})}$	${\text{f}}_{x(x^{2}-3y^{2})}$

In generale possiamo semplificare nei calcoli che ci interessano per l’ibridizzazione indicando gli orbitali nel modo seguente

1 S 2S 2Px 2Py 2Pz

IBRIDIZZAZIONE DEGLI ORBITALI ATOMICI

l’IBRIDIZZAZIONE è un metodo matematico cioè una combinazione lineare (somma o differenza di orbitali atomici puri) che ci permette di dare una spiegazione ad alcuni dati sperimentali che sarebbero impossibili da giustificare utilizzando gli orbitali atomici puri.

Cominciamo con un esempio semplice : il METANO

il metano ha formula CH4

dati sperimentali :

a) 4 legami con energia identica quindi il C deve avere 4 elettroni disponibili per i legami con 4 atomi di H

b) angoli di legame di 109° ( quindi ha forma tetraedrica)

se il C dovesse utilizzare gli orbitali atomici puri avremmo qualche problema, infatti il C ha 2 elettroni spaiati negli orbiltali 2Px e 2Py

1S² 2S² 2Px¹ 2Py¹

la presenza di 2 elettroni spaiati negli orbitali p indica che dovrebbe formare 2 soli legami con l’H ma sappiamo che nel metano il C usa 4 legami infatti forma CH4.

Inoltre, se il C utilizzasse gli orbitali puri dovremmo avere 3 legami con uguale energia ( a causa degli orbitali Px Py Pz che hanno energia identica tra loro) ed un legame con energia più bassa a causa dell’orbitale 2S.

Non solo, ma i 3 orbitali P sono orientati nello spazio secondo gli assi cartesiani cioè con un angolo di 90° e non di 109°come invece si osserva sperimentalmente nel metano.

Pertanto se si usassero gli orbitali puri del C non avremmo nessuna corrispondenza con ciò che invece osserviamo sperimentalmente.

COSA POSSIAMO FARE PER SPIEGARE I DATI SPERIMENTALI?

Per dare una giustificazione ai dati sperimentali ricorriamo ad un ESPEDIENTE MATEMATICO cioè un semplice calcolo che viene definito ibridizzazione degli orbitali atomici.

(ATTENZIONE!!! l’ibridizzazione NON E’ UN FENOMENO CHE AVVIENE IN REALTA’ ma è solo un metodo matematico che i chimici utilizzano per giustificare i dati sperimentali!!!)

L’ibridizzazione di n orbitali atomici produce alla fine del calcolo n nuovi orbitali detti orbitali ibridi che sostituiti nell’equazione di Schrödinger danno come risultato un valore di energia identica.

procediamo con il calcolo degli orbitali ibridi del C

supponiamo che gli orbitali atomici puri si mescolino ( essendo essi funzioni matematiche possiamo sommarli tra loro)

T1 = a1S + b1X +c1Y + d1 Z

T2 = a2S + b2X +c2Y + d2 Z

T3 = a3S + b3X +c3Y + d3 Z

T4 = a4S + b4X +c4Y + d4 Z

in questo caso a,b,c,d rappresentano la parte di orbitale che si mescola con gli altri.

proseguiamo al calcolo di a,b,c,d ricordandoci che :

la meccanica quantistica ci dice che le funzioni d’onda devono essere normalizzate in quanto la somma dei quadrati di Ψ( che rappresenta la probabilità di trovare l’elettrone intorno al nucleo) deve essere la certezza cioè il 100% quindi

∫Ψ² dt =1

(condizione di normalizzazione)

e se si hanno due funzioni Ψ diverse tra loro allora

∫Ψa Ψ_bdt =0

(condizione di ortogonalità)

si deduce che possiamo scrivere

ai² + bi²+ci² +di²=1 dove in questo caso i = 1,2,3,4

e che

aiaj +bibj +cicj +didj =0 dove il prodotto ij è (1,2) (1,3) (1,4 )

in conseguenza si deve avere anche

a1²+ a2²+ a3² +a4² =1

b1² b2²+b3²+b4²=1

c1²+c2²+c3²+c4²=1

d1²+d2²+d3²+d4² =1

a1b1+a2b2+a3b3+a4b4 =0

——- etc per i 4 orbitali ibridi.

queste forme matematiche ci saranno utili nel calcolo dei coefficienti a,b,c,d che rappresentano il grado di contributo di ogni orbitale puro nell”orbitale ibrido.

la forma dell’orbitale ibrido è data dal coefficiente a infatti

t = as+bx+cy+dz =as + √1-a2 p

la relazione che lega l’angolo tra due orbitali ibridi è :

cos Θij = bibj +cicj+didj / √bi²+ci²+di²√bj²+cj²+dj²

nel caso specifico del metano (come anche per lo ione ammonio) i 4 ibridi sono della stessa natura quindi

a1=a2=a3=a4

calcoliamo i coefficienti dalla relazione

a1²+ a2²+ a3² +a4² =1

essendo a1=a2=a3=a4

a1² = 1

a1 =1/2

se consideriamo il sistema seguente

risultano le relazioni

b1=c1=d1 e b2=c2 essendo Δ2 proiettato sulla bisettrice dell’asse xOy

ne consegue che

a1²+b1²+c1²+d1²= 1

1/4 + 3b1² = 1

b1=c1=d1 = ± 1/2

avendo scelto t1 che punta nella direzione positiva degli assi x,y,z si ha :

b1=c1=d1= 1/2

pertanto l’orbitale ibrido

T1 = 1/2(S+ X + Y + z)

per calcolare T2 ricordiamo che

T2= 1/2 S + b2(x+y)+dz Z

per le condizioni di normalità e di ortogonalità

1/4+ 2b2² +d2²=1

1/4 +1/2 b2 + 1/2 b2 +1/2 d2 =0

cioè 2b2² +d2²=3/4

b2 + 1/2 d2 = -1/4

eliminando b2 tra le due equazioni abbiamo

12d2²+4d2- 5 = 0

le cui radici sono +1/2 e – 5/6

se consideriamo l’orbitale Δ2 consideriamo che sia orientato verso l’alto quindi scegliamo d2=1/2 per cui b2= -1/2

in definitiva l’orbitale

T2 = 1/2(S -X-Y + Z)

per calcolare T3 e T4 scriviamo

b1²+b2²+b3² +b4² =1

a1b1+a2b2+a3b3+a4b4= 1

b3²+b4²=1/2

b3=- b4

b3²=b4²=1/4

prendiamo b3= +1/2 b4 = -1/2 avremo

T3= 1/2S + 1/2 X +c3Y + d3 Z

T4 = 1/2 S – 1/2 X + c4 Y +d4 Z

e per calcolare c3 e d3 scriviamo che T3 è ortogonale a T2 e T1

1/4 + 1/4 +1/2 c3 +1/2 d3 =0

1/4-1/4 -1/2 c3 +1/2 d3 =0

da cui si deduce che c3=d3 = – 1/2

analogamente per c4 e d4 si ha

c4=1/2 d4 = – 1/2

i 4 orbitali ibridi ottenuti sono quindi

T1 =1/2(s +x+y+z)

T2 =1/2(s -x-y+z)

T3 =1/2(s -x-y-z)

T4 =1/2(s -x+ y-z)

calcolo degli angoli di legame

cos Θij = bibj +cicj+didj / √bi²+ci²+di²√bj²+cj²+dj²

porta a 4 angoli di 109°5′

cioè il metano CH4 ha struttura spaziale tetraedrica e possiede 4 legami con energia uguale come osservato sperimentalmente