STRUTTURA DELL’ATOMO: il modello quantistico

Verificato che il modello atomico di Bohr- Somerfeld non era valido, c’era da chiedersi come fosse possibile rappresentare un atomo o meglio come si potesse descrivere l’elettrone che si trova attorno al nucleo.La risposta a questa domanda è che si può rappresentare l’elettrone in un atomo solamente in termini di probabilità utilizzando la meccanica quantistica.

Consideriamo l’atomo di idrogeno costituito dal nucleo e da un solo elettrone e supponiamo che la sua posizione sia rappresentata da un punto nello spazio ad una certa distanza r dal nucleo  e che il nucleo si trovi all’origine  o  di un sistema di assi cartesiani x,y,z

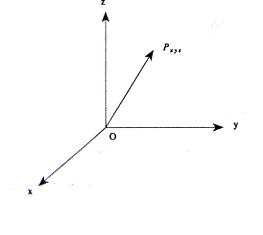
Supponiamo che l’elettrone fermo, si trovi in un punto P (vedi figura) caratterizzato dai valori x,y,z. Supponiamo, adesso,  che l’elettrone si muova intorno al nucleo ed occupi una nuova posizione P1 che è caratterizzata dai valori X1,Y1,Z1 e supponendo si muova ancora, assumerà una posizione caratterizzata dai valori di X2,Y2,Z2. Pertanto la posizione dell’elettrone è caratterizzato da P che dipende dai valori di X,Y,Z cioè P è funzione di X,Y,Z. C’è però un problema: nel momento stesso in cui diciamo l’elettrone si trova in un punto P= f(X,Y,Z) esso si è già mosso e avrà assunto una nuova posizione P= f(X1,Y1,Z1). E’ evidente che in questo modo non possiamo descrivere il moto dell’elettrone perchè non possiamo conoscere da che parte esso si muova anche se sappiamo che con certezza si muove intorno al nucleo. 

L’ unico modo è individuare un punto nello spazio intorno al nucleo, caratterizzato dalla funzione delle coordinate di x,y,z, cioè   ψ = f (x,y,z)    e valutare quante volte l’elettrone ha la probabilità di passare per quel punto ogni 100 volte. 

Come è possibile calcolare questa probabilità ? Ci viene in aiuto la matematica che ci dice che se conosciamo le coordinate del punto intorno al nucleo,  cioè se conosciamo  ψ = f (x,y,z)  allora elevando al quadrato la funzione matematica che descrive l’elettrone in quel punto otterremo un risultato compreso tra 0 ed 1 e quindi il suo valore indica che la funzione è proporzionale alla probabilità di trovare l’elettrone in quel punto.. Per esempio, nota la funzione dell’elettrone nel punto X1,Y1,Z1,  ψ = f (X1,Y1,Z1) se eleviamo al quadrato ed otteniamo il risultato ψ² = f (X1,Y1,Z1) = 0  ciò significa che l’elettrone nel suo movimento intorno al nucleo non passerà mai per quel punto, mentre se invece si ha  ψ² = f (X1,Y1,Z1) = 0,11 allora significa che su 100 volte l’elettrone passerà 11 volte da quel punto.

Possiamo sostenere che, mentre la funzione ψ non ha significato fisico potendo assumere qualunque valore numerico, il suo quadrato ψ² rappresenta la probabilità di trovare l’elettrone in quel punto. Se ripetiamo il procedimento per un numero molto elevato di punti intorno al nucleo otterremo per ogni punto un valore sempre compreso tra 0 ed 1 . Sappiamo inoltre con certezza che l’elettrone si trova sicuramente intorno al nucleo perciò se sommiamo tutti i valori di probabilità calcolati intorno al nucleo tale somma deve essere la certezza di trovare l’elettrone certezza che numericamente deve rappresentare il 100 % cioè 1.Pertanto 

∫ ψ² δτ = 1 

che è uno dei 2 postulati della meccanica quantistica. La somma è rappresentata dal segno  di integrale ∫ e non dal segno ∑  poichè   ψ descrive  valori discreti e non continui. Dobbiamo dire ancora che se si hanno 2 funzioni  ψ diverse cioè   ψa  e  ψb  esse si definiscono ORTOGONALI se   

∫ ψa ψb  δτ  =  0 

abbiamo così trovato le due condizioni fondamentali della meccanica quantistica cioè

1. la condizione di NORMALIZZAZIONE 

                                 ∫ ψa ψa  δτ  = 1  

                                 ∫ ψb ψb  δτ  = 1  

2)  la condizione di ORTOGONALITA’

 ∫ ψa ψb  δτ  = 0  

 ∫ ψb ψa  δτ  =  0  

La meccanica quantistica ci permette, quindi, di ottenere la distribuzione dell’elettrone intorno al nucleo.

EQUAZIONE DI SHRODINGER  E CALCOLO DELL’ENERGIA DEGLI ELETTRONI

Supponiamo di dover misurare il peso di un corpo : per far questo adoperiamo uno strumento chiamato bilancia e lo applichiamo al corpo in esame .Il risultato è il peso del corpo. Supponiamo ancora di dover misurare la densità di un liquido, adoperiamo, allo scopo, uno strumento detto densimetro che applichiamo al liquido ed il risultato fornito è la densità.

Sin quì abbiamo considerato delle entità fisiche(il corpo,il liquido) cui abbiamo applicato uno strumento materiale quali bilancia e densimetro ed il risultato è stato il valore di ciò che volevamo misurare cioè il peso e la densità. Se adesso consideriamo una funzione matematica  quale ad esempio

  Y = X²

e supponiamo di voler calcolare la RADICE QUADRATA di questa funzione. A tal fine occorre applicare, in questo caso,  uno strumento matematico chiamato operatore che possa permettere il calcolo del risultato. Come sappiamo, l’operatore radice quadrata è il simbolo √ che applicato alla funzione dà come risultato la radice quadrata  cioè

 Y =√ X²     = X 

Possiamo notare che l’applicazione dell’ Operatore Radice Quadrata alla funzione X² modifica la funzione originaria dando origine ad una nuova funzione diversa dalla prima (infatti si ottiene X).

Supponiamo di avere la stessa funzione originaria

Y = X²  

e supponiamo di voler ottenere il risultato di una moltiplicazione della funzione per un numero ad es. 2.

Per far questo adoperiamo l’ Operatore 2 x

quindi applichiamo l’operatore 2x alla funzione X² ed avremo

Y= 2x X²

il cui risultato è 2X² .

Notiamo che in questo secondo caso l’ Operatore  x 2 non ha modificato la funzione originaria trasformandola ma l’ ha semplicemente moltiplicata per una costante( 2 ) mentre la funzione è rimasta X².

Ciò ci permette di concludere che esistono in matematica operatori che applicati alle funzioni forniscono il risultato dell’operazione ma che trasformano la funzione originaria ed altri, invece, che non trasformano la funzione originaria ma la moltiplicano semplicemente per una costante.

Supponiamo adesso di voler calcolare l’Energia di un elettrone, caratterizzato dalla funzione matematica  ψ . 

Anche in questo caso, adoperiamo un operatore, l’ OPERATORE ENERGIA   che viene indicato con H  definito  operatore Hamiltoniano.

Se applichiamo l’operatore energia alla funzione ψ che descrive l’elettrone, vediamo che tale operatore lascia la funzione immutata, moltiplicandola per una costante che, seppur non sia propriamente l’energia,  ha le dimensioni di un’energia per cui possiamo definirla come l’Energia dell’elettrone E

Hψ = E ψ

questa espressione è

L’ EQUAZIONE D’ONDA DI SHRODINGER  CHE CI PERMETTE DI CALCOLARE L’ENERGIA DI UN ELETTRONE IN UN ATOMO.

 C’è da chiedersi però quale sia la forma analitica della funzione  ψ su cui applicare l’operatore energia H.

Per trovare la forma analitica di  ψ è più opportuno  utilizzare al posto delle coordinate cartesiane x,y,z un nuovo sistema di coordinate : le coordinate polari che quì rappresentiamo.

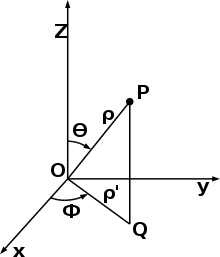
tra le coordinate cartesiane e quelle polari vi sono le relazioni