I GAS : LA LEGGE DI BOYLE

LO STATO GASSOSO

Lo stato gassoso ideale è uno stato della materia in cui  atomi o molecole sono ritenute puntiformi e non sono sottoposte a forze di attrazione o di repulsione di alcun genere. Se i gas si trovano in uno stato tale da essere  lontani dalla liquefazione e siano sufficientemente rarefatti, essi tendono a comportarsi quasi tutti allo stesso modo, indipendentemente dalla natura del gas. Questo ha permesso di considerare un gas “perfetto” se si trova in condizioni di bassa pressione ed alta temperatura. In un gas perfetto, le forze interatomiche o intermolecolari tra le singole particelle di una sostanza gassosa  sono così piccole che non c’è più un’effettiva coesione per cui gli atomi o le molecole del gas sono liberi di muoversi con una certa velocità ed in forma caotica e ne consegue che  le particelle atomiche o molecolari del gas si urtano continuamente l’una con  l’altra.  Il gas, quindi, non ha un volume proprio definito ma tende ad occupare tutto lo spazio del recipiente in cui è contenuto e assume la forma del contenitore. Quando studiamo i gas dobbiamo considerare :

1.  la pressione 

2.   la temperatura

3.  la massa

4.   il volume

5.   numero di moli

in quanto queste proprietà  sono in relazione tra loro e determinano lo stato del gas.

LA PRESSIONE DI UN GAS

Consideriamo un gas ideale cioè un gas costituito da particelle puntiformi e che tra esse non vi siano attrazioni o repulsioni (gas ideale). Esse si muovono caoticamente con una certa velocità cioè possiedono una quantità di moto data da MASSA X VELOCITA’= mV.

Quando le molecole di gas si scontrano con le pareti di un contenitore, come mostrato in figura,

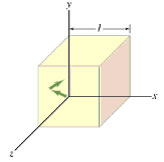
le molecole producono una forza perpendicolare alla parete. La somma delle forze che tutte le molecole esercitano sulla superficie della parete è definita  PRESSIONE. Matematicamente 

PRESSIONE= P = FS

Assumendo che le collisioni molecole-parete siano elastiche, cioè che dopo l’urto sia conservata la quantità di moto, la velocità V delle 1,2,3….N molecole di gas lungo un solo asse (ad es.l’asse x)è data da:

V_x = v_1x  + v2x + v3x +…+V_Nx

supponiamo che sia L la distanza tra 2 pareti quindi  la variazione del momento mv che indichiamo con P  sarà   Δp= 2 mVx

se Δt è il tempo impiegato dalle N molecole per collidere con due pareti allora FΔt = 2mVx

essendo  Δt = 2L /Vx sostituendo avremo:

F=2mVx2LVx

per cui   

F=mv2L

ricordando che V_x =V_1x + V_2x…V_Nx

F= mNV²_x / L

la velocità che qui appare è la media del quadrato delle velocità da non confondere con la velocità quadratica media delle molecole.

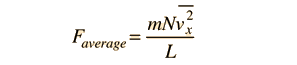
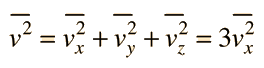
che in termini di Energia cinetica media è  :            

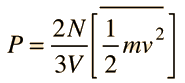
PV = NmVx23

 dove Vx è la media delle velocità delle molecole.

cioè  3PV = NmV_x²      se dividiamo ambedue i membri per 2 si ha      

32PV =NmVx22

e ricordando che Ecin = 1/2 mV² si può scrivere   

32PV = N Ecin

sapendo inoltre che PV =NkT  allora   3/2 NkT = NEcin    da cui

E_cin = 3/2 kT

k è la costante di Boltzman e T la temperatura assoluta.

Bisogna però mettere in evidenza che questo risultato è valido solo per i gas monoatomici.

LA LEGGE DI BOYLE    (A  t =K)

Un’osservazione attenta mostra che Pressione e Volume sono correlate l’una all’altra ed i valori di queste proprietà determinano lo stato del gas. A metà del 1600, Robert Boyle studiò la relazione tra la pressione p e il volume V di un gas in un recipiente MANTENUTO AD UNA TEMPERATURA COSTANTE.   L’ osservazione che fece Boyle è che in un recipiente di volume V che contiene un gas ad una pressione P, se si raddoppia la pressione il volume diminuisce sino a divenire la metà, se la pressione diventa 3 volte quella iniziale il Volume diminuisce e diviene 1/3 di quello iniziale.

Supponiamo che la pressione sia 1 atm ed il volume del gas iniziale è 4 litri. Quando la pressione è 1,33 il volume diventa 3 litri; se la pressione è P= 2 allora V=2 se la pressione è 3 allora V= 1.33 Se in questo esempio si moltiplicano tra loro P e V si ottiene sempre lo stesso valore 4, infatti 1 x 4 = 4   1,33 x 3 = 3,999=4  2×2 = 4   3 x 1,33 =4  Si può generalizzare dicendo che   il prodotto PV= K  che è la forma generale della legge di Boyle che si può anche scrivere P = k/V cioè la pressione è inversamente proporzionale al volume e viceversa.

Se rappresentiamo in un grafico la P sulle ordinate ed il volume sulle ascisse otteniamo un’iperbole

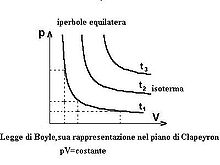
La figura successiva mostra l’animazione di ciò che avviene comprimendo un gas (comprimere significa aumentare la pressione):

LA PRESSIONE ED IL VOLUME DI UN GAS IN DUE CONDIZIONI DIVERSE

Se consideriamo un gas a T=k con pressione P1 e volume V1  avremo  P1 x V1 =K    e se modifichiamo la pressione da P1 a P2 dovremo avere  P2x V2=K 

e quindi possiamo scrivere   

 P1 V1 = P2 V2   

da cui è possibile ottenere il nuovo volume occupato dal ga alla pressione P2 infatti

P2= P1 V1 / P2

Conoscendo 3 dei parametri è quindi possibile ottenere il quarto.

FACCIAMO UN ESEMPIO::

Un gas si trova alla pressione di 2,5 atmosfere ed occupa un volume di 2 litri. Quale sarà la pressione se il volume diviene 1,5 litri?

quindi P1= 2,5 atm   V1= 2,5 litri   P2 =?  V2= 1,5    pertanto

essendo  P1V1= P2V2       allora P2 = P1V1/ V2  P2= 2,5 x 2 /  1,5 = 3,3 atm

ESERCIZI SULLA LEGGE DI BOYLE

1-Un gas ha un volume e una pressione iniziale di 3 m3 e di 5 atm. Mantenendo costante la temperatura quale sarà in suo volume alla pressione di 15 atm?
Soluzione
La trasformazione del gas avviene a temperatura costante ed è quindi  isoterma per cui si applica la legge di Boyle

Condizioni iniziali del gas   P1= 5 atm     V1 = 3 m³

Condizioni finali del gas      P2= 15 atm   V2 = da calcolare

Sappiamo che P1V1 = K  e che P2V2 = K per cui si può scrivere
P1V1=P2V2    da cui si ottiene   V2 = P1V1/P2  e sostituendo i valori  corrispondenti si ha 

V2 = 5 atm • 3 m3 /15 atm = 1 m³

2-Un gas occupa un volume di 6,0 L alla temperatura di 60 °C. Sapendo che la pressione iniziale del gas è di 2,8 atm e che la temperatura non varia, determina la pressione necessaria per portare il volume a 2,5 L?
Soluzione
Anche in questo caso abbiamo una trasformazione isoterma (infatti la temperatura rimane costante) quindi per la legge di Boyle si ha:

P1 = 2,8 atm    V1= 6,0 L

P2 = da calcolare   V2 = 2,5 L

pertanto essendo P1V1=K e P2V2=K   allora P1V1=P2V2 da cui si calcola P2

P2=P1V1/V2

P2= 2,8 atm •6,0 L/2,5 L =6,7 atm